Celestial Navigation – The Celestial Sphere

/ October 5, 2016

Once upon a time people thought that the earth was the centre of the universe and that the sun and stars all revolved around us (sounds a bit like one of my ex-boyfriends).

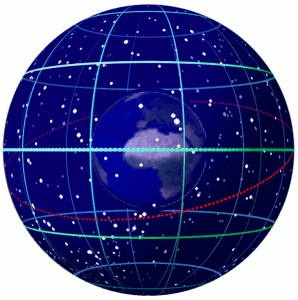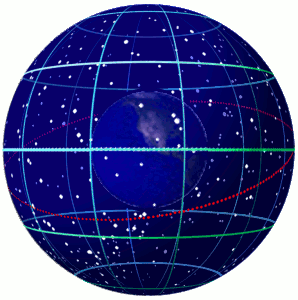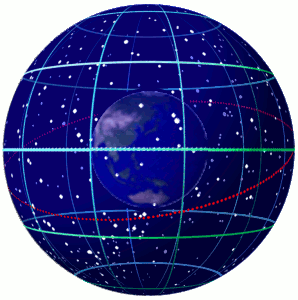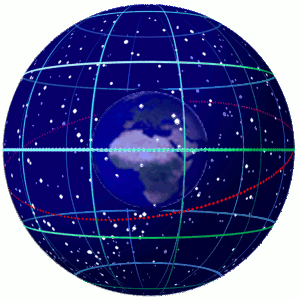
These ancient people started mapping the sun and the stars on to a sphere – the Celestial Sphere – basically it is a concept.

So imagine the Earth is a small ball, and then imagine we are hovering inside a big balloon. Now imagine that all the stars are painted on the inside of the balloon – that balloon is the Celestial Sphere.

It is much easier to imagine the stars mapped like this – than a billion stars in an infinite universe.

Here on earth we have got a grid pattern to identify whereabouts we are on the globe – this is called Latitude and Longitude. The Celestial Sphere – or the inside of that balloon also has a grid which maps the location of all the Celestial Bodies. Instead of being called Latitude and Longitude the grid is called Declination and Hour Angle. The Sphere also has a celestial equator and celestial poles.

So let’s regroup for a minute:

  • Declination – is equivalent to parallel lines of Latitude
  • Greenwich Hour Angle (GHA) – is equivalent to meridians of Longitude
  • Celestial Equator – is equivalent to the earth’s equator
  • Celestial Poles – are equivalent to the earth’s poles

Are you with me so far?

There has to be exceptions (of course…) With Longitude on earth we measure that in degrees East or West of Greenwich – up to 180º in each direction. Whereas with Greenwich Hour Angle (GHA), we measure that westward to 360º – from the Prime Meridian.

You can work out the difference between Longitude and Greenwich Hour Angle as follows:

GHA = Longitude W or 360º – Longitude E

(Don’t worry if you don’t understand this just yet – I am hoping it will all become clear soon!)

Earth_within_celestial_sphere.gif

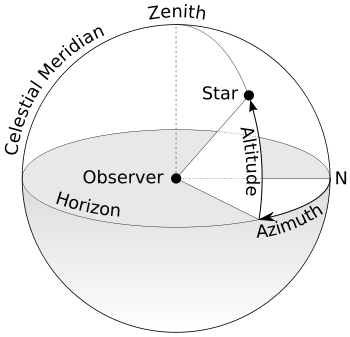
Stop for a minute, go outside and look straight up in to the sky – directly above your head, the area on the celestial sphere directly above you is called the Zenith – z – and the area where you are standing is called the Ground Position.

Likewise the point directly beneath a star on the Earth’s surface is the Ground Position of that star.

When we use our Sextant to measure the angle between the horizon and a star, we are measuring it’s Altitude.

When we note the exact UTC time that we take that measurement, we can work out the position of that star – or it’s ground position in that moment of time.

Our aim is to measure the shortest distance between the ground position of the star and the ground position of the observer.

 

350px-azimuth-altitude_schematic-svg

Now if you paid more attention than I did in high school maths, then you might want to do some more research on all the geometry behind this concept.

But very basically if you look at the diagram above you can see that the angle between the Zenith of the observer and the Horizon is 90º – ok got that.

We then measure with our sextant that the angle between the horizon and the star is say 40º. We then deduct that from 90º to obtain the missing angle between the star and our Zenith – which in this case must be 50º.

By using tables we can figure out the ground position of that star at that particular time. If we set our dividers to a distance of 50º (more info on how to do that later) and draw a circle around the ground position of the star – we have got a position circle – we are somewhere on that line.

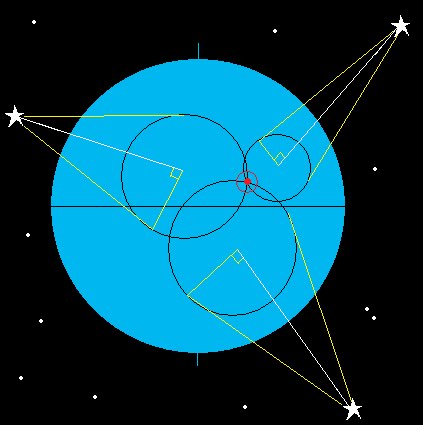
3-circles-of-equal-altitude

The trouble is that this circle could be a huge diameter and if our position could be anywhere on there it isn’t a particularly accurate fix! With one sight we can obtain a position line but to get a fix we need an intersection of two or more lines as per the diagram above – this can come from two or more different celestial bodies at the same time, or the same body at different times.

Quick Quiz

  1. What is a Zenith?
  2. What is Declination?
  3. What is an Altitude?
  4. How do you work out the difference between the Altitude and the observer’s zenith?
  5. What does GHA stand for?
  6. Describe the celestial sphere
  7. What is the equivalent of Latitude on the Celestial sphere?
  8. What is the difference between Longitude and GHA?

 

Tune in next time when we go back to basics with plotting positions, dead reckoning, position circles and all that kind of thing.

If you want to revise the Sextant post – click here

If you want to swot up about Time and why that is so important – click here

Thanks for following! Please comment, make suggestions and ask questions in the section below. 🙂

Related posts

28 thoughts on “Celestial Navigation – The Celestial Sphere”

  1. Pingback: Celestial Navigation – Sextant Angle Corrections | Astrolabe Sailing

  2. Pingback: Celestial Navigation – Where is the Sun? | Astrolabe Sailing

  3. Pingback: Navigation – Position Lines | Astrolabe Sailing

  4. Pingback: Celestial Navigation – Putting it all Together | Astrolabe Sailing

  5. Pingback: Ocean Yachtmaster | Astrolabe Sailing

  6. Pingback: Celestial Navigation- Measurement of Time | Astrolabe Sailing

  7. If the ground position of the star is known (from the celestial sphere / tables), then why not just take an equally accurate compass bearing to the star (which will be the same as to its ground position) as this singularly intersects the circle (obtained from the angle between it and the observer’s zenith) at the observer’s ground point ?

    Liked by 1 person

    Reply

      • I don’t know, as I’m here on your website to learn. ( Thank you 😉 ) Tbh., I’ve only handled a sextant once, many, many years ago, and I don’t remember seeing a compass built into it. It just seemed logical when I looked at your diagram, as it would be very much more accurate to use a radial line (intersecting your circle at 90 degrees) than two other arcs whose angle of crossing is so small.

        I haven’t yet read all your pages on the subject, so I don’t yet know how your position is worked out when a sighting is just taken on the sun ..as no other celestial bodies can be seen.? It’s time for me to do some more study within your pages ..to try and find the answer to that one :))

        Liked by 1 person

      • Lol! I’ll do some research too. I hope you enjoy my notes. I’m definitely not an expert on celestial nav. Just a very keen student who is always learning! I’m heading away racing this weekend, but will dig out my books when I get back and ponder your question!
        Cheers Viki 🙂

        Liked by 1 person

  8. There is no possibility of “an equally accurate compass bearing” when compared to the radius of the circle (the observer’s zenith distance) Compasses are accurate to ±½° at best while a sextant is accurate to ±1/2 minute of arc or better. an example is that you could know the radius of the circle to an accuracy of ±1/2 nm, but the position along the circumference of the circle to ±30nm. A 60nm range in position is just not good enough. That is why we shoot multiple stars so that the 1 nm thick circles can intersect.

    Liked by 1 person

    Reply

  9. Thank you
    I’m in the middle of an Astro navigation course and was struggling with the EP CP calculations.
    Your clear instructions was very helpful 👍

    Liked by 1 person

    Reply

  11. To whom it may concern.

    I want to show how longitude can be determined by astronomical
    observations. For this I need information about the angle between
    the Greenwich Merack angle at midnight for every day of the year.
    With that the longitude can be determined for northern latitudes.

    I hope that you can direct me to such data. Since determining
    longitude by astronomical data is presently considered not
    possible it would be a needed paper to correct that misconception
    in the scientific community.

    If you can help I hope that you will find it to be your duty to help in this
    endeavor since you are so involved in astronomy.

    I have contacted a Dr. at De Paul University whose comment on my proof is
    I see your point, give an example. Now I need astronomical data about the
    big dipper and it’s relation to Polaris for each day of the year.

    I hope this note peaks your interest in helping me. Thank you for reading my
    note and I hope to hear from you promptly.

    Cordially

    Joe Kmiec
    815-436-7729
    jekmiec@sbcglobal.net

    Like

    Reply

    • Hi Joe,
      Thanks for your question, I definitely don’t consider myself an expert – more of a keen student too. Are you looking for the tables? Or are you looking for something else?

      Like

      Reply

  13. I cannot understand what is “noon sight” when I need to shoot the sun, if I need noon sight? At 12:00:00 local time? Or I can do 12:10:00 local time, for example?

    Liked by 1 person

    Reply

    • Good question and I am a bit rusty to be honest as its been a few years since I wrote this and I haven’t practiced in ages. I think the noon-site is done when the sun is highest in the sky. I am pretty sure I did another post about noon-sites?

      Like

      Reply

      • Hello. This is RYA advice:
        Noon site should be taken at noon, when the sun is at the highest point in the sky.
        For doing sights in the real world you need the equation of time for today. If you don’t have that to hand you can estimate when the sun will be at its highest based on your current longitude and then adding on or taking away the appropriate time if you are east or west of the Greenwich meridian. As you know, the sun is directly above the Greenich meridian at roughly 1200UT every day. Best way to do it is to calculate when. the ‘merpass’ will be for your current longitude and then set yourself up say 15 minutes before. Keep taking sun sights until you see the sun dipping again. Draw a graph of your results and interpolate to get the best result for noon.

        Liked by 1 person

Leave a comment

This site uses Akismet to reduce spam. Learn how your comment data is processed.